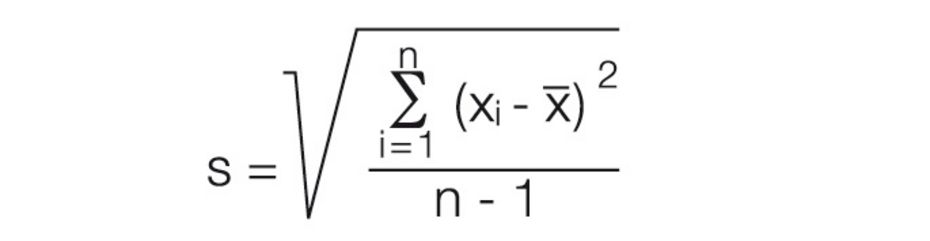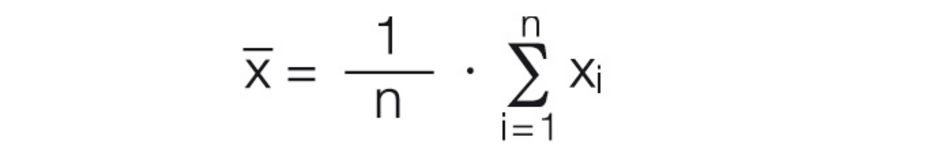La garantie d'une qualité de production constante requiert des outils précis et des mécanismes de contrôle. Du fait de l'intensification des normes et réglementations en matière de responsabilités des fabricants, les obligations de documentation de qualité sont vouées à augmenter. L'industrie automobile est à l'avant-garde de cette tendance, et a contraint ses nombreux fournisseurs à adopter des mesures similaires. Ces règles de documentation s'appliquent notamment à notre technologie de vissage.
En plus de calculer et d'afficher plusieurs variables (couple, angle, profondeur, couple de friction, etc.), il est également nécessaire d'effectuer une évaluation statistique des résultats d'assemblage.
Il existe plusieurs modèles de distributions mathématiques. Les points de vissage peuvent être facilement représentés à l'aide de la distribution gaussienne standard, qui présente l'avantage d'être bien connue et simple à calculer.
Série mesures :
Une série de mesure se réfère à la réalisation de plusieurs mesures dans des conditions constantes. Pour obtenir des données statistiquement significatives, une série d'au moins 10 mesures est nécessaire, à savoir qu'une série de 50 mesures est encore préférable.
Ecart-type :
L'écart-type d'une série de mesures est la différence moyenne des valeurs de mesure individuelles par rapport à la moyenne calculée. L'écart-type est calculé selon la formule suivante :
La plage d’écarts standard est toujours ± comprise comme intervalle.
Habituellement, la précision d'un instrument de mesure ou d'un outil est spécifiée avec un écart type relatif. Cet écart-type relatif est aussi important pour la détermination d'autres quantités statistiques.
Signification des caractéristiques de distribution normale :
La valeur moyenne d'une série de mesures est la valeur qui a le plus de probabilités de se rapprocher de la valeur réelle. Ce postulat ne s'applique uniquement si l'on dispose d'un nombre de mesures assez grand. Dans la pratique, le nombre de 10 valeurs mesurées s'est avéré être le minimum nécessaire. Si une série de mesures ne détecte que des erreurs aléatoires, les résultats se répartiront le long d'une distribution normale gaussienne. D'après cette courbe de distribution, le postulat suivant peut être fait sur la base des relations mathématiques :
68,26 % de toutes les mesures se trouveront dans une plage de +/- 1 ET
95,44 % toutes les mesures se trouveront dans une plage de +/- 2 ET
99,73 % toutes les mesures se trouveront dans une plage de +/- 3 ET
99,99 % toutes les mesures se trouveront dans une plage de +/- 4 ET
Tous ces postulats ne peuvent fournir qu'une probabilité, et jamais une valeur absolue.
A ce stade, la déclaration disant que des couples peuvent être maintenus avec une précision de <± 3 % d'écart-type mérite une clarification. La valeur de 3 % est calculée en tant que pourcentage de l'écart type par rapport à la valeur moyenne correspondante. Les expériences pratiques ont néanmoins démontré que les les visseuses DEPRAG assurent généralement une précision de couple supérieure à cette valeur.