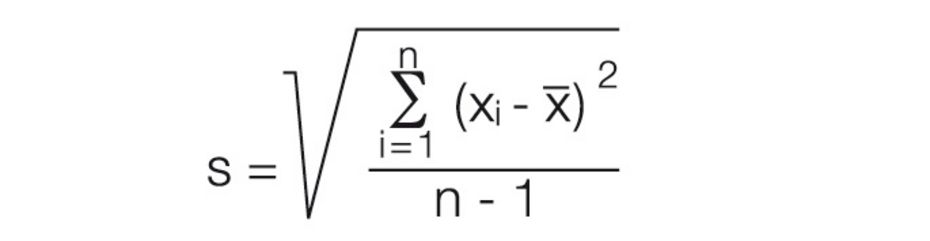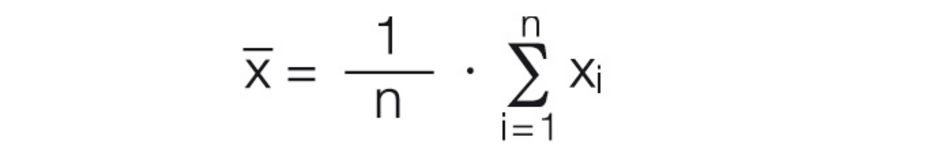Statistische Grundlagen
in der Schraubtechnik
Die Einhaltung einer gleichbleibenden Fertigungsqualität erfordert den Einsatz genauester Fertigungsmittel sowie geeigneter Kontrollmechanismen. Durch neue, strenger gefasste Bestimmungen zur Produkthaftung werden dabei die Anforderungen an die Dokumentation der Fertigungsqualität auch weiterhin steigen. Insbesondere die Automobilindustrie hat hierbei eine Vorreiterrolle übernommen und zwingt Zulieferer zu ähnlichen Maßnahmen. Dies gilt in besonderem Maße auch für das automatische Verschrauben.
Neben der Auswahl geeigneter Messgrößen (Anzugsmoment, Drehwinkel, Schraubtiefe, Furchmoment, etc.) geht es dabei vor allem um die statistische Beurteilung der erzielten Ergebnisse.
Im Folgenden werden die statistische Grundlagen vorgestellt, die zur Bewertung von Ergebnissen in der Schraubtechnik herangezogen werden.
Gauß'sche Normalverteilung
Es existieren eine Reihe verschiedener mathematischer Verteilungsmodelle. Die Verschraubungen lassen sich am einfachsten durch die Normalverteilung nach Gauß darstellen, die als bekannteste Verteilung auch den Vorteil relativ einfacher mathematischer Zusammenhänge bietet.
Messreihe:
Die Messreihe bezeichnet eine Reihe von Messwerten, die unter den gleichen Bedingungen ermittelt wurden. Für die Gewinnung statistischer Aussagen ist die Mindestgröße der Messreihe 10 Werte, besser noch sind 50 Werte.
Standardabweichung:
Die Standardabweichung der Messreihe ist definiert als die mittlere Differenz einzelner Messwerte bezogen auf den errechneten Mittelwert. Die Standardabweichung s wird nach folgender Formel berechnet:
Der Wertebereich der Standardabweichung wird immer als ± Intervall verstanden.
Üblicherweise wird die Genauigkeit eines Messgerätes oder eines Werkzeuges mit der relativen Standardabweichung angegeben. Sie ist auch für die Ableitung weiterer statistischer Größen von zentraler Bedeutung.
Bedeutung der Kenndaten der Normalverteilung:
Der Mittelwert der Messreihe ist der Wert, der dem wahren Wert mit der größten Wahrscheinlichkeit am nächsten liegt. Diese Aussage gilt nur unter der Einschränkung einer hinreichend großen Zahl von Messwerten. Im praktischen Gebrauch hat sich die Zahl von 10 Messwerten als die mindestens notwendige herausgestellt. Werden mit einer Messreihe ausschließlich die zufälligen Fehler erfasst, wird sich die Verteilung der Ergebnisse nach der Gauß'schen Normalverteilung einstellen. Nach dieser Verteilungskurve kann aufgrund der mathematischen Zusammenhänge folgende Aussage getroffen werden:
68,26 % aller Messwerte werden in einem Bereich von ±1s liegen
95,44 % aller Messwerte werden in einem Bereich von ±2s liegen
99,73 % aller Messwerte werden in einem Bereich von ±3s liegen
99,99 % aller Messwerte werden in einem Bereich von ±4s liegen
Alle diese Aussagen können immer nur eine gewisse Wahrscheinlichkeit angeben, niemals jedoch eine absolute Angabe sein.
An dieser Stelle soll die Aussage, dass Drehmomente mit einer Genauigkeit von <± 3 % Standardabweichung eingehalten werden können, präzisiert werden. Die Angabe der 3 % ist als prozentuale Angabe der Standardabweichung durch Bezug auf den zugehörigen Mittelwert errechnet. Praktische Versuche zeigen, dass dieser Wert in vielen Fällen bei DEPRAG Schraubwerkzeugen weit unterschritten wird.