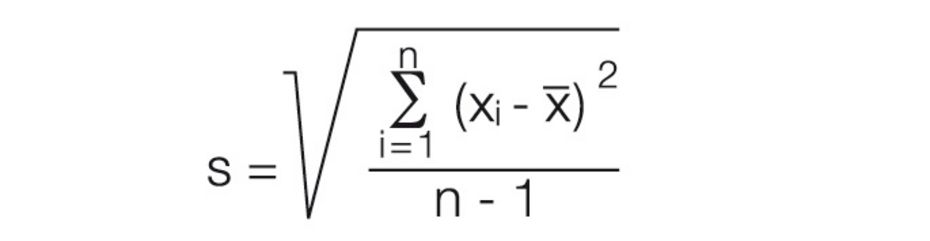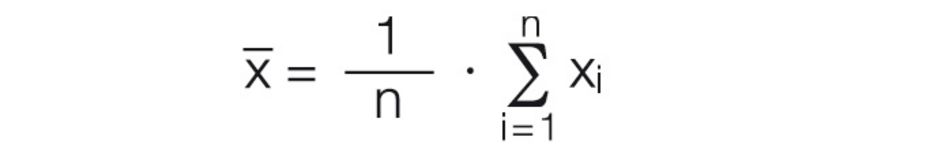To retain an equal and permanent production quality, exact production means as well as suitable control-mechanisms are necessary. Through new and stricter regulations in the product liability area, the requirements in regards to quality documentation will continue to rise. Especially the automotive industry has taken on a forerunner role in this matter and has enforced its numerous suppliers to take similar measures. This documentation measure applies in particular to our screwdriving technology.
Besides the need to display a selection of suitable measuring units (torque, angle, depth, friction-torque, etc.) it is also necessary to statistically evaluate the assembly results.
There are several mathematical distribution models. The screw-assemblies can be easily displayed using the well-known Gaussian standard distribution, which has the advantage that this method is well known and requires relative simple mathematics.
Measurement Series:
The measurement series is a series of measuring values, which were determined using identical conditions. To obtain a statistical statement, a test series of a minimum of 10 values is required; however using 50 values is even better.
Standard Deviation:
The standard deviation of a test series is determined by the average difference of individual measuring values in connection to the calculated average value. The standard deviation is calculated according to the following formula:
The value range of the standard deviation is always understood as ± interval.
Usually, the precision of a measuring instrument or a tool is indicated using a relative standard deviation. This relative standard deviation is of primary importance when derive additional statistical sizes.
Understanding the characteristics of the standard deviation:
The average value of a measuring series is the value, which in all probability comes closest to the actual value. This statement is only valid if an adequately large number of measuring values have been used. In the practical application, the number of 10 measuring values has shown to be the minimum requirement. If a measuring series acquires solely the random errors, then the distribution of the results fall within the Gaussian standard deviation. According to the distribution curve, the following statement can be made because of the mathematical context:
68,26 % of all measurements will be in a range of +/- 1 s
95,44 % of all measurements will be in a range of +/- 2 s
99,73 % of all measurements will be in a range of +/- 3 s
99,99 % of all measurements will be in a range of +/- 4 s
All these statements can only indicate a certain probability, never however an absolute.
At this point, the statement of the accuracy of <± 3 % Standard Deviation is further clarified. The value of 3 % is calculated as a percentage statement from the standard deviation by referencing the applicable average value. Practical tests have however shown, that in many cases of the DEPRAG Screwdrivers, this accuracy value is actually lower than 3 %.